Crescimento E Decrescimento De Uma Função Do 1 Grau Exemplo: Compreender como funções de primeiro grau crescem ou decrescem é fundamental para diversas áreas, desde a modelagem de fenômenos físicos até a análise de dados econômicos. Neste artigo, exploraremos a influência do coeficiente angular na inclinação da reta, analisaremos gráficos e resolveremos problemas práticos, desvendando o comportamento dessas funções essenciais da matemática.
A forma geral de uma função do 1º grau é representada por f(x) = ax + b, onde ‘a’ é o coeficiente angular e ‘b’ o coeficiente linear. O coeficiente angular determina a inclinação da reta: se ‘a’ for positivo, a função é crescente; se ‘a’ for negativo, a função é decrescente. O coeficiente linear indica o ponto de interseção da reta com o eixo y.
Através de exemplos práticos e gráficos, iremos ilustrar como identificar o crescimento ou decrescimento, calcular valores de x e y, e aplicar esses conceitos em situações reais.
Crescimento e Decrescimento de Funções do 1º Grau: Crescimento E Decrescimento De Uma Função Do 1 Grau Exemplo
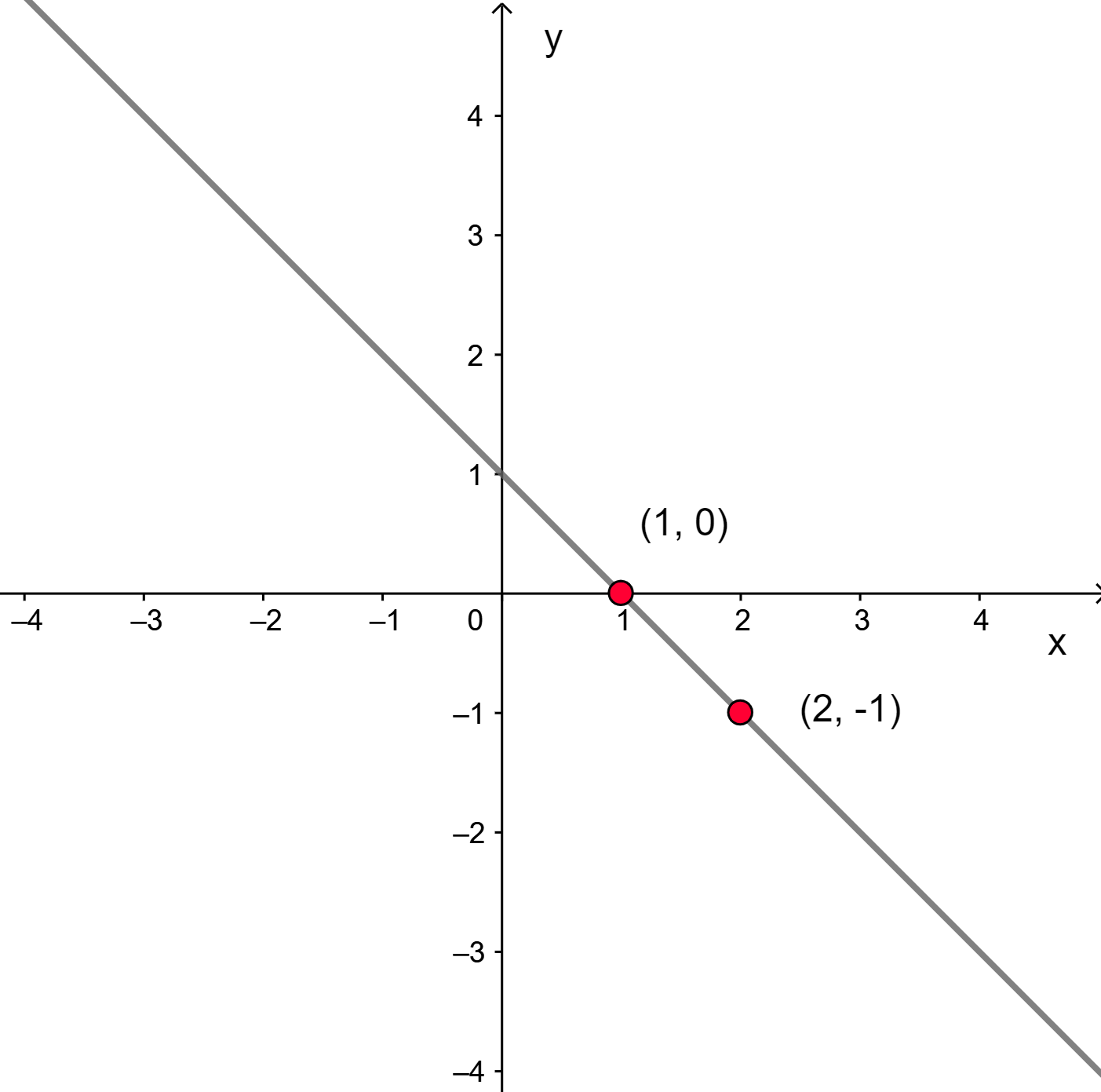
As funções do 1º grau, também conhecidas como funções lineares, são ferramentas matemáticas essenciais para modelar diversas situações reais, desde o cálculo de custos e lucros até o estudo de movimentos uniformes. Compreender seu crescimento e decrescimento é fundamental para a interpretação e aplicação dessas funções.
Introdução ao Crescimento e Decrescimento de Funções do 1º Grau, Crescimento E Decrescimento De Uma Função Do 1 Grau Exemplo
Uma função do 1º grau tem a forma geral f(x) = ax + b, onde ‘a’ é o coeficiente angular e ‘b’ é o coeficiente linear. O coeficiente angular (a) determina a inclinação da reta que representa a função no plano cartesiano. Se ‘a’ for positivo, a função é crescente; se ‘a’ for negativo, a função é decrescente. O coeficiente linear (b) representa o ponto onde a reta intersecta o eixo y (quando x = 0).
Uma função crescente apresenta valores de f(x) que aumentam à medida que x aumenta. Uma função decrescente, por sua vez, apresenta valores de f(x) que diminuem à medida que x aumenta.
Exemplo de função crescente: f(x) = 2x +
1. Seu gráfico é uma reta ascendente. Exemplo de função decrescente: f(x) = -x +
3. Seu gráfico é uma reta descendente. Imagine um gráfico para cada uma: a reta da função crescente sobe da esquerda para a direita, enquanto a reta da função decrescente desce da esquerda para a direita.
| Equação | Coeficiente Angular (a) | Coeficiente Linear (b) | Crescimento/Decrescimento |
|---|---|---|---|
| f(x) = 2x + 1 | 2 | 1 | Crescente |
| f(x) = -x + 3 | -1 | 3 | Decrescente |
Analisando o Gráfico de uma Função do 1º Grau
A análise gráfica de uma função do 1º grau permite a identificação imediata de seu crescimento ou decrescimento. Uma reta ascendente (da esquerda para a direita) indica uma função crescente, enquanto uma reta descendente indica uma função decrescente.
O coeficiente angular (a) pode ser determinado pela inclinação da reta, calculada pela razão entre a variação de y e a variação de x entre dois pontos quaisquer da reta. O coeficiente linear (b) é o valor de y no ponto onde a reta intersecta o eixo y. Os pontos de interseção com os eixos x e y são encontrados resolvendo a equação para x = 0 (interseção com o eixo y) e y = 0 (interseção com o eixo x).
Exemplo: Considere a função f(x) = 2x –
4. Seu gráfico é uma reta que intercepta o eixo y em (0, -4) e o eixo x em (2, 0). O coeficiente angular é 2, indicando uma função crescente. Imagine o gráfico: uma reta ascendente cruzando o eixo y em -4 e o eixo x em 2.
Resolvendo Problemas com Funções do 1º Grau
As funções do 1º grau são utilizadas para resolver diversos problemas envolvendo relações lineares entre duas variáveis. A seguir, são apresentados exemplos de problemas e suas resoluções:
- Problema 1 (Função Crescente): Uma empresa de táxis cobra R$ 5,00 de taxa inicial e R$ 2,00 por quilômetro rodado. Qual o custo de uma corrida de 10 km?
- Problema 2 (Função Decrescente): A temperatura de um forno diminui 5°C a cada minuto após ser desligado. Se a temperatura inicial era de 200°C, qual será a temperatura após 15 minutos?
- Problema 3 (Comparação de Crescimento): Duas empresas oferecem planos de internet. A empresa A cobra R$ 50,00 fixos mais R$ 10,00 por GB de dados. A empresa B cobra R$ 30,00 fixos mais R$ 15,00 por GB. Para qual quantidade de GB o plano da empresa A é mais vantajoso?
Resolução dos problemas:
- Problema 1: f(x) = 2x + 5. Para x = 10 km, f(10) = 2(10) + 5 = R$ 25,00
- Problema 2: f(x) = -5x + 200. Para x = 15 minutos, f(15) = -5(15) + 200 = 125°C
- Problema 3: Comparando as funções f(x) = 10x + 50 e g(x) = 15x + 30, encontramos o ponto de interseção (x = 4 GB). Para valores de GB abaixo de 4, o plano A é mais vantajoso.
Aplicações Práticas de Funções do 1º Grau

As funções do 1º grau são amplamente aplicadas em diversas áreas do conhecimento. Sua simplicidade e capacidade de modelar relações lineares tornam-nas ferramentas poderosas para a resolução de problemas em contextos reais.
Em física, por exemplo, são utilizadas para descrever movimentos uniformes. Em economia, auxiliam na análise de custos e lucros. Na engenharia, são empregadas em projetos de estruturas e circuitos.
Exemplo: O custo de produção de um certo produto é dado por C(x) = 10x + 500, onde x é o número de unidades produzidas. A receita obtida com a venda é dada por R(x) = 20x. O lucro é dado por L(x) = R(x)
-C(x) = 10x – 500.
A modelagem matemática, através de funções do 1º grau, permite uma análise precisa e eficiente de problemas complexos, auxiliando na tomada de decisões em diversos contextos.
Comparação entre Funções Crescentes e Decrescentes
Funções crescentes e decrescentes do 1º grau se diferenciam principalmente pelo sinal do coeficiente angular (a). Funções crescentes possuem ‘a’ > 0, enquanto funções decrescentes possuem ‘a’ < 0. Isso resulta em gráficos com inclinações diferentes: a reta de uma função crescente sobe da esquerda para a direita, e a reta de uma função decrescente desce da esquerda para a direita.
| Função Crescente | Função Decrescente |
|---|---|
| Coeficiente angular (a) > 0 | Coeficiente angular (a) < 0 |
| Gráfico ascendente | Gráfico descendente |
| Valores de y aumentam com o aumento de x | Valores de y diminuem com o aumento de x |

