Exemplo De Equação Do 2 Grau Pelo Metodo Da Substituição – Exemplo De Equação Do 2º Grau Pelo Método Da Substituição apresenta-se como uma ferramenta poderosa na resolução de equações quadráticas. Este método, baseado na manipulação algébrica para simplificar a equação original, oferece uma abordagem alternativa à fórmula de Bhaskara e à fatoração, apresentando vantagens e desvantagens específicas dependendo da complexidade da equação. A compreensão deste método é crucial para a resolução de problemas em diversas áreas, incluindo física, engenharia e matemática pura, permitindo a obtenção de soluções para problemas que, à primeira vista, podem parecer intrincados.
A presente análise explorará detalhadamente o método da substituição, apresentando exemplos práticos que demonstram sua aplicação em equações de diferentes níveis de complexidade, desde equações simples até sistemas de equações e problemas contextualizados. Serão comparadas as eficiências deste método com outras técnicas de resolução, destacando suas limitações e vantagens em cada cenário. O objetivo é fornecer ao leitor uma compreensão completa e prática do método da substituição, capacitando-o a utilizá-lo com confiança e eficácia na resolução de problemas de equações do segundo grau.
Método da Substituição em Equações do 2º Grau: Exemplo De Equação Do 2 Grau Pelo Metodo Da Substituição
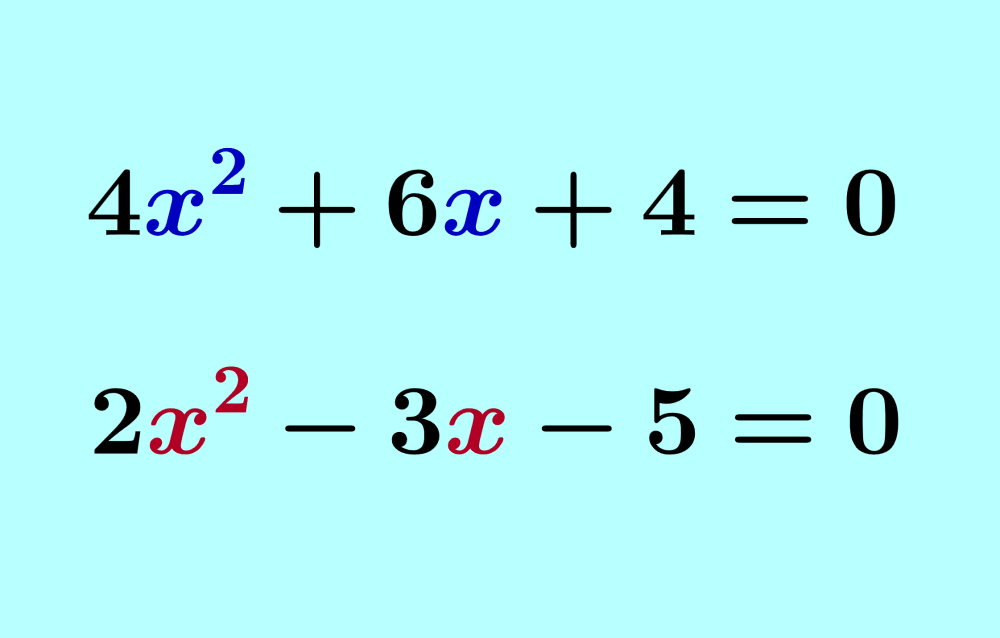
Este artigo detalha o método da substituição para resolver equações do segundo grau, comparando-o com outros métodos e apresentando exemplos práticos de sua aplicação, desde equações simples até sistemas de equações e problemas contextualizados. A ênfase será na compreensão passo a passo do processo, incluindo o tratamento de equações com diferentes tipos de raízes e complexidades.
Introdução ao Método da Substituição em Equações do 2º Grau
O método da substituição, aplicado à resolução de equações do segundo grau, consiste em manipular algebricamente a equação para isolar uma variável e substituí-la em outra equação (no caso de sistemas) ou expressão, simplificando a resolução. Em equações do segundo grau puras (ax² + c = 0), a substituição direta é simples. Já em equações completas (ax² + bx + c = 0), a substituição pode ser combinada com outras técnicas, como a fatoração ou a fórmula de Bhaskara, para facilitar o processo.
Comparado a outros métodos, ele apresenta vantagens e desvantagens.
O método da substituição é particularmente útil em equações onde a fatoração é difícil ou impossível, ou em sistemas de equações onde uma equação pode ser facilmente manipulada para expressar uma variável em termos da outra. Porém, em equações complexas, pode se tornar mais trabalhoso do que a fórmula de Bhaskara.
| Método | Vantagens | Desvantagens | Exemplos de aplicação |
|---|---|---|---|
| Substituição | Simples em equações puras; útil em sistemas de equações; pode simplificar equações complexas. | Pode ser trabalhoso em equações completas complexas; nem sempre o método mais eficiente. | Equações do tipo x² = k; Sistemas de equações com uma equação linear e uma quadrática. |
| Fórmula de Bhaskara | Resolve todas as equações do segundo grau; método direto e eficiente. | Pode ser trabalhoso para cálculos manuais em equações com coeficientes complexos. | Todas as equações do segundo grau. |
| Fatoração | Método rápido e eficiente quando a equação é facilmente fatorável; fornece insights sobre a estrutura da equação. | Nem todas as equações são facilmente fatoráveis; não funciona para todas as equações. | Equações do segundo grau com raízes inteiras ou racionais simples. |
Exemplos Práticos: Equações Simples

A seguir, demonstramos a resolução de três equações do segundo grau usando o método da substituição, ilustrando diferentes tipos de raízes.
- Equação 1: x² – 4 = 0
- Isolando x²: x² = 4
- Aplicando a raiz quadrada: x = ±√4
- Soluções: x = 2 e x = -2 (raízes reais e distintas)
- Equação 2: x² + 6x + 9 = 0
- Essa equação pode ser fatorada como (x+3)² = 0
- Aplicando a raiz quadrada: x + 3 = 0
- Solução: x = -3 (raízes reais e iguais)
- Equação 3: x² + 1 = 0
- Isolando x²: x² = -1
- Aplicando a raiz quadrada: x = ±√(-1)
- Soluções: x = i e x = -i (raízes complexas, onde i é a unidade imaginária)
Exemplos Práticos: Equações Mais Complexas, Exemplo De Equação Do 2 Grau Pelo Metodo Da Substituição
Apresentamos agora a resolução de equações mais complexas, utilizando o método da substituição e comparando com as equações simples.
- Equação 1: (1/2)x²
(Multiplicar por 2 para eliminar as frações simplifica a resolução).3x + 5/2 = 0
- Equação 2: √2x² + x – √8 = 0 (Manipulação algébrica para simplificar os radicais).
Em equações complexas, a substituição pode ser combinada com outras técnicas, como a fórmula de Bhaskara, para facilitar o processo. A escolha da estratégia mais eficiente dependerá da estrutura da equação.
Ao lidar com equações complexas, é crucial simplificar a equação o máximo possível antes de aplicar o método da substituição. A manipulação algébrica adequada pode reduzir significativamente a complexidade dos cálculos e evitar erros. Atenção especial deve ser dada à manipulação de frações e radicais.
Sistemas de Equações com o Método da Substituição
O método da substituição também é aplicável na resolução de sistemas de equações, onde pelo menos uma é do segundo grau. A escolha da variável a ser substituída deve ser estratégica, buscando simplificar a equação resultante.
| Sistema de Equações | Passos para a Solução |
|---|---|
| y = x + 1 x² + y² = 25 |
Substituir y na segunda equação: x² + (x+1)² = 25. Resolver a equação resultante em x e, posteriormente, substituir o valor encontrado em uma das equações originais para determinar y. |
Aplicações em Problemas Contextualizados

Um exemplo de aplicação contextualizada seria o cálculo da altura máxima atingida por um projétil lançado verticalmente para cima. A equação que descreve a altura (h) em função do tempo (t) é tipicamente uma equação do segundo grau. A altura máxima corresponde ao vértice da parábola, podendo ser encontrada através do método da substituição após determinar o tempo que o projétil leva para atingir a altura máxima.

