Números Decimais: Operações e Exemplos – Matemática Básica. Embarque conosco numa jornada fascinante pelo universo dos números decimais! Descubra como esses números, aparentemente simples, são a chave para entendermos o mundo ao nosso redor, desde as finanças do dia a dia até os cálculos mais complexos da ciência. Prepare-se para desvendar os segredos da adição, subtração, multiplicação e divisão de decimais, aplicando esses conhecimentos em situações práticas e resolvendo problemas do cotidiano com facilidade e confiança.
Aprender matemática nunca foi tão envolvente!
Vamos explorar os conceitos fundamentais, diferenciando números decimais finitos e infinitos, e compreendendo sua representação fracionária e percentual. Através de exemplos práticos e tabelas ilustrativas, você dominará as operações com números decimais, aplicando-as em situações reais, como cálculos de áreas, gestão financeira e medições. Ao final desta jornada, você terá a segurança e a habilidade para lidar com os números decimais em qualquer situação, com fluidez e precisão.
Conceitos Fundamentais de Números Decimais

Embarque conosco numa fascinante jornada pelo universo dos números decimais! Nesta seção, desvendaremos os mistérios por trás dessa representação numérica tão presente em nosso dia a dia, desde o cálculo do troco até a compreensão de dados científicos complexos. Prepare-se para admirar a elegância e a praticidade desse sistema que nos permite expressar quantidades com precisão e detalhe.
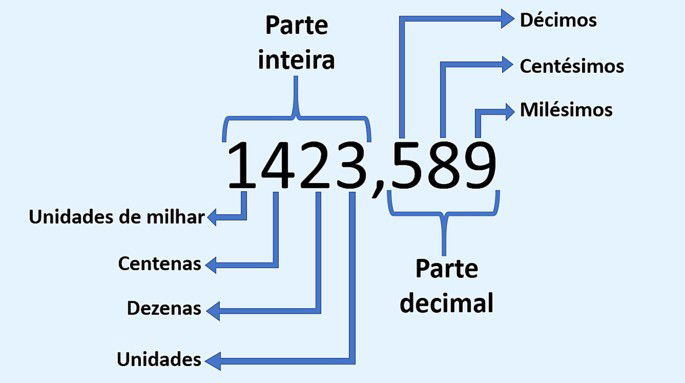
A representação decimal de um número é uma forma de expressá-lo utilizando o sistema de numeração decimal, que se baseia na potência de dez. Cada dígito em um número decimal ocupa uma posição específica, representando uma potência de dez. A vírgula separa a parte inteira da parte decimal, indicando a posição das unidades. À esquerda da vírgula, temos as unidades, dezenas, centenas, e assim por diante; à direita, temos os décimos, centésimos, milésimos, e assim sucessivamente.
Essa estrutura permite representar frações de forma concisa e eficiente.
Diferença entre Números Decimais Finitos e Infinitos, Números Decimais: Operações E Exemplos – Matemática Básica
A principal distinção entre números decimais finitos e infinitos reside no comprimento de sua parte decimal. Números decimais finitos possuem uma parte decimal com um número limitado de dígitos após a vírgula. Por exemplo, 2,5; 3,14; e 10,005 são números decimais finitos. Já os números decimais infinitos, como o próprio nome sugere, possuem uma parte decimal com infinitos dígitos após a vírgula.
Esses dígitos podem se repetir em um padrão (números decimais infinitos periódicos) ou não (números decimais infinitos não periódicos). Um exemplo clássico de número decimal infinito periódico é 1/3 = 0,333…, enquanto √2 é um exemplo de número decimal infinito não periódico.
O Sistema de Numeração Decimal e sua Relação com os Números Decimais
O sistema de numeração decimal, também conhecido como sistema de base 10, é fundamental para a compreensão dos números decimais. Este sistema utiliza dez dígitos (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) para representar qualquer número. A posição de cada dígito determina seu valor posicional, que é uma potência de dez. A vírgula decimal estende esse sistema para representar partes menores que uma unidade, utilizando potências negativas de dez.
A relação é intrínseca: o sistema decimal fornece a estrutura para representar os números decimais, permitindo expressar tanto quantidades inteiras quanto frações com precisão.
Exemplos de Números Decimais, suas Representações Fracionárias e em Porcentagem
A tabela a seguir ilustra a versatilidade dos números decimais, mostrando sua equivalência em diferentes representações:
| Número Decimal | Representação Fracionária | Representação em Porcentagem |
|---|---|---|
| 0,5 | 1/2 | 50% |
| 0,25 | 1/4 | 25% |
| 0,75 | 3/4 | 75% |
| 1,2 | 6/5 | 120% |
Operações com Números Decimais: Números Decimais: Operações E Exemplos – Matemática Básica
Embarque conosco numa jornada fascinante pelo universo dos números decimais! Após compreendermos seus conceitos fundamentais, agora é hora de desvendar o poder e a elegância das operações com esses números que permeiam nosso cotidiano, desde as compras no supermercado até os cálculos mais complexos da engenharia. Prepare-se para dominar as adições, subtrações, multiplicações e divisões, desvendando seus segredos e aplicando-os com maestria.
Adição e Subtração de Números Decimais
A adição e subtração de números decimais seguem um princípio fundamental: a organização alinhada das vírgulas. Imagine as vírgulas como pontos de referência, garantindo que unidades, décimos, centésimos e assim por diante se somem ou subtraiam corretamente. A precisão é a chave!Exemplo de Adição: 23,45 + 1,8 = 25,Observe que as vírgulas estão perfeitamente alinhadas, facilitando o cálculo.
Outro exemplo, com quantidades diferentes de casas decimais: 12,7 + 3,256 = 15,956. Para facilitar, podemos adicionar zeros à direita do número com menos casas decimais sem alterar seu valor (12,700 + 3,256).Exemplo de Subtração: 45,67 – 12,3 = 33,Novamente, o alinhamento das vírgulas é crucial. Outro exemplo com diferentes casas decimais: 100,5 – 23,125 = 77,375.
(100,500 – 23,125). A subtração, assim como a adição, exige atenção ao posicionamento dos valores.
Multiplicação de Números Decimais
A multiplicação de números decimais, embora pareça mais complexa à primeira vista, é um processo elegante e lógico. Inicialmente, ignore as vírgulas e realize a multiplicação como se fossem números inteiros. Após obter o resultado, conte o número total de casas decimais presentes nos fatores originais. Esse número total indica quantas casas decimais devem ser separadas no resultado final, a partir da direita.Exemplo com números inteiros e decimais: 2,5 x 3 = 7,5 (uma casa decimal no fator 2,5).
Outro exemplo: 3,14 x 2,2 = 6,908 (duas casas decimais no total, uma em cada fator). A multiplicação de decimais nos permite explorar o mundo das áreas e volumes com precisão.
Divisão de Números Decimais
A divisão de números decimais pode apresentar diferentes cenários, incluindo a presença ou ausência de resto. Um método eficaz é eliminar a vírgula do divisor, multiplicando-o por uma potência de 10 (10, 100, 1000, etc.). O mesmo fator deve ser multiplicado pelo dividendo. Em seguida, realiza-se a divisão como com números inteiros.
| Dividendo | Divisor | Quociente | Resto |
|---|---|---|---|
| 25,5 | 5 | 5,1 | 0 |
| 12,75 | 2,5 | 5,1 | 0 |
| 34,8 | 7 | 4,97 | 1 |
| 15,2 | 3,8 | 4 | 0 |
Comparação entre Operações com Números Decimais e Inteiros
As operações com números decimais compartilham semelhanças fundamentais com as operações correspondentes em números inteiros: o processo básico de adição, subtração, multiplicação e divisão permanece o mesmo. A principal diferença reside no tratamento da vírgula e das casas decimais. Em números inteiros, a posição de cada dígito representa uma potência de 10 (unidades, dezenas, centenas, etc.), enquanto em números decimais, a vírgula divide a parte inteira da parte fracionária, com cada casa decimal representando potências negativas de 10 (décimos, centésimos, milésimos, etc.).
A precisão e o alinhamento são essenciais nas operações com decimais, garantindo resultados corretos.
Aplicações e Exemplos de Números Decimais no Cotidiano
Os números decimais, embora possam parecer abstratos em um contexto puramente matemático, são ferramentas essenciais que permeiam nosso dia a dia, facilitando inúmeras transações e compreensões do mundo ao nosso redor. Sua presença discreta, mas fundamental, se manifesta em situações corriqueiras, desde as compras no supermercado até os cálculos de projetos de engenharia. Vamos explorar alguns exemplos concretos de como esses números decimais moldam nossa realidade.
Exemplos Práticos do Uso de Números Decimais
A utilização de números decimais se mostra imprescindível em diversas áreas do nosso cotidiano. Imagine, por exemplo, a compra de alimentos no supermercado: o preço de um quilo de tomates, frequentemente expresso em reais com centavos (R$ 5,75), é um número decimal. Da mesma forma, o peso de um produto, medido em quilogramas ou gramas, também pode ser representado por um número decimal (1,25 kg de arroz).
No contexto financeiro, os números decimais são fundamentais para representar valores monetários com precisão, incluindo taxas de juros, salários e investimentos. A medição de distâncias, volumes e temperaturas também utiliza extensivamente os decimais, assegurando maior precisão em diversos contextos.
Problemas com Operações Decimais em Contextos Reais
Vamos analisar alguns problemas práticos que envolvem operações com números decimais:
Problema 1: Maria comprou 2,5 kg de maçãs a R$ 8,90 o quilo e 1,8 kg de bananas a R$ 5,20 o quilo. Quanto Maria gastou ao todo?
Solução: Primeiro, calculamos o custo das maçãs: 2,5 kg
– R$ 8,90/kg = R$ 22,
25. Em seguida, calculamos o custo das bananas: 1,8 kg
– R$ 5,20/kg = R$ 9,
36. Finalmente, somamos os custos: R$ 22,25 + R$ 9,36 = R$ 31,61. Maria gastou R$ 31,61.
Problema 2: Um pedreiro precisa cortar uma tábua de 3,75 metros de comprimento em três partes iguais. Qual o comprimento de cada parte?
Solução: Dividimos o comprimento total pelo número de partes: 3,75 m / 3 = 1,25 m. Cada parte terá 1,25 metros de comprimento.
Cálculo da Área de um Retângulo com Medidas Decimais

Para calcular a área de um retângulo, multiplicamos a medida da base pela medida da altura. Se um retângulo tem base de 4,2 metros e altura de 2,8 metros, sua área será:
Área = base x altura = 4,2 m x 2,8 m = 11,76 m²
Portanto, a área do retângulo é de 11,76 metros quadrados.
Representação de Grandezas Físicas com Números Decimais
Os números decimais são cruciais na representação precisa de grandezas físicas. Por exemplo, a massa de um objeto pode ser expressa em quilogramas (kg) com decimais (ex: 2,5 kg), o comprimento em metros (m) (ex: 1,85 m), o volume em litros (L) (ex: 3,7 L), e a temperatura em graus Celsius (°C) (ex: 25,5 °C). Essa precisão decimal permite medições mais refinadas e cálculos mais exatos em diversas áreas da ciência e da engenharia.
A utilização de números decimais em grandezas físicas assegura a precisão necessária para aplicações que demandam exatidão, como na construção civil, na medicina e em experimentos científicos.

